Mệnh đề
MỆNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN
A. Tóm tắt lí thuyết
1.Định nghĩa:
Mệnh đề là một câu khẳng định Đúng hoặc Sai .
Một mệnh đề không thể vừa đúng hoặc vừa sai
2.Mệnh đề phủ định:
Cho mệnh đề . Mệnh đề “Không phải
” gọi là mệnh đề phủ định của
.
Ký hiệu là . Nếu P đúng thì
sai, nếu
sai thì
đúng
3. Mệnh đề kéo theo và mệnh đề đảo
Cho hai mệnh đề và
. Mệnh đề “nếu
thì
” gọi là mệnh đề kéo theo
Ký hiệu là . Mệnh đề
chỉ sai khi P đúng Q sai
Cho mệnh đề . Khi đó mệnh đề
gọi là mệnh đề đảo của
4. Mệnh đề tương đương
Cho hai mệnh đề và
. Mệnh đề “
nếu và chỉ nếu
” gọi là mệnh đề tương đương
Ký hiệu là .
Mệnh đề đúng khi cả
và
cùng đúng
Chú ý: “Tương đương” còn được gọi bằng các thuật ngữ khác như “điều kiện cần và đủ”, “khi và chỉ khi”, “nếu và chỉ nếu”.
5. Mệnh đề chứa biến
Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập nào đó mà với mỗi giá trị của biến thuộc
ta được một mệnh đề.
Ví dụ: “
chia hết cho
” với
là số tự nhiên
:”
” Với
là số thực
6. Các kí hiệu 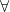 ,
,  và mệnh đề phủ định của mệnh đề có chứa kí hiệu
và mệnh đề phủ định của mệnh đề có chứa kí hiệu 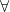 ,
, .
.
Kí hiệu “: đọc là với mọi, $: đọc là tồn tại
Phủ định của mệnh đề “ ” là mệnh đề “
”
Phủ định của mệnh đề “ ” là mệnh đề “
”
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
DẠNG 1: XÁC ĐỊNH MỆNH ĐỀ VÀ TÍNH ĐÚNG SAI CỦA MỆNH ĐỀ .
Ví dụ 1: Các câu sau đây,có bao nhiêu câu là mệnh đề?
(1) Ở đây đẹp quá!
(2) Phương trình vô nghiệm
(3) 16 không là số nguyên tố
(4) Hai phương trình và
có nghiệm chung.
(5) Số có lớn hơn
hay không?
(6) Italia vô địch Worldcup 2006
(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.
(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.
A.4 B.6 C.7 D.5
Lời giải:
Câu (1) và (5) không là mệnh đề(vì là câu cảm thán, câu hỏi)
Các câu (3), (4), (6), (8) là những mệnh đề đúng
Câu (2) và (7) là những mệnh đề sai.
Ví dụ 2: Cho ba mệnh đề sau, với là số tự nhiên
(1) là số chính phương
(2) Chữ số tận cùng của là 4
(3) là số chính phương
Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng mệnh đề nào sai?
A. mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai
B. mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai
C. mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai
D. mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai
Lời giải:
Ta có số chính phương có các chữ số tận cùng là. Vì vậy
– Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là đúng thì có chữ số tận cùng là 2 nên không thể là số chính phương. Vậy trong hai mệnh đề này phải có một mệnh đề là đúng và một mệnh đề là sai.
– Tương tự, nhận thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì có chữ số tận cùng là 3 nên không thể là số chính phương.
Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
DẠNG 2: CÁC PHÉP TOÁN VỀ MỆNH ĐỀ .
Các phép toán mệnh đề được sử dụng nhằm mục đích kết nối các mệnh đề lại với nhau tạo ra một mệnh đề mới. Một số các phép toán mệnh đề là : Mệnh đề phủ định(phép phủ định), Mệnh đề kéo theo(phép kéo theo), mệnh đề đảo, mệnh đề tương đương(phép tương đương).
Các ví dụ minh họa.
Ví dụ 1: Nêu mệnh đề phủ định của các mệnh đề sau, cho biết mệnh đề này đúng hay sai?
+ ” Hình thoi có hai đường chéo vuông góc với nhau”
A. ” Hai đường chéo của hình thoi không vuông góc với nhau”, mệnh đề này đúng
B. ” Hai đường chéo của hình thoi vuông góc với nhau”, mệnh đề này sai
C. ” Hai đường chéo của hình thoi vuông góc với nhau”, mệnh đề này đúng
D. ” Hai đường chéo của hình thoi không vuông góc với nhau”, mệnh đề này sai
+ ” 6 là số nguyên tố”
A. ” 6 là số nguyên tố”, mệnh đề này đúng
B. ” 6 không phải là số nguyên tố”, mệnh đề này sai
C. ” 6 là số nguyên tố”, mệnh đề này sai
D. ” 6 không phải là số nguyên tố”, mệnh đề này đúng
+ ” Tổng hai cạnh của một tam giác lớn hơn cạnh còn lại”
A. ” Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại”, mệnh đề này đúng
B. ” Tổng hai cạnh của một tam giác lớn hơn hoặc bằng cạnh còn lại”, mệnh đề này sai
C. ” Tổng hai cạnh của một tam giác lớn hơn hoặc bằng cạnh còn lại”, mệnh đề này đúng
D. ” Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại”, mệnh đề này sai
+ ”
”
A. ”
“, mệnh đề này đúng
B. ”
“, mệnh đề này sai
C. ”
“, mệnh đề này đúng
D. ”
“, mệnh đề này sai
+ ” Phương trình
có nghiệm ”
A. ” phương trình
có nghiệm “, mệnh đề này sai
B. ” phương trình
vô nghiệm “, mệnh đề này sai
C. ” phương trình
vô nghiệm “, mệnh đề này đúng
D. ” phương trình
có nghiệm “, mệnh đề này đúng
+ ”
”
A. ”
“, mệnh đề này đúng
B. ”
“, mệnh đề này đúng
C. ”
“, mệnh đề này sai
D. ”
“, mệnh đề này sai
Lời giải:
Ta có các mệnh đề phủ định là
” Hai đường chéo của hình thoi không vuông góc với nhau”, mệnh đề này sai
” 6 không phải là số nguyên tố”, mệnh đề này đúng
” Tổng hai cạnh của một tam giác nhỏ hơn hoặc bằng cạnh còn lại”, mệnh đề này sai
”
“, mệnh đề này sai
” phương trình
vô nghiệm “, mệnh đề này đúng vì
”
“, mệnh đề này sai
Ví dụ 2: Phát biểu mệnh đề và phát biểu mệnh đề đảo, xét tính đúng sai của nó.
a) ” Tứ giác
là hình thoi” và
” Tứ giác
AC và BD cắt nhau tại trung điểm mỗi đường”
A. Mệnh đề là ” Nếu tứ giác
là hình thoi thì AC và BD cắt nhau tại trung điểm mỗi đường”, mệnh đề này sai.
Mệnh đề đảo là : “Nếu tứ giác
có AC và BD cắt nhau tại trung điểm mỗi đường thì
là hình thoi “, mệnh đề này đúng.
B. Mệnh đề là ” Nếu tứ giác
là hình thoi thì AC và BD cắt nhau tại trung điểm mỗi đường”, mệnh đề này đúng.
Mệnh đề đảo là : “Nếu tứ giác
có AC và BD cắt nhau tại trung điểm mỗi đường thì
là hình thoi “, mệnh đề này sai.
C. Mệnh đề là ” Nếu tứ giác
là hình thoi thì AC và BD cắt nhau tại trung điểm mỗi đường”, mệnh đề này đúng.
Mệnh đề đảo là : “Nếu tứ giác
có AC và BD cắt nhau tại trung điểm mỗi đường thì
là hình thoi “, mệnh đề này sai.
D. Mệnh đề là ” Nếu tứ giác
là hình thoi thì AC và BD cắt nhau tại trung điểm mỗi đường”, mệnh đề này đúng.
Mệnh đề đảo là : “Nếu tứ giác
có AC và BD cắt nhau tại trung điểm mỗi đường thì
là hình thoi “, mệnh đề này sai.
b) và
A. Mệnh đề là ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
sai.
Mệnh đề đảo là : ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
đúng.
B. Mệnh đề là ” Nếu
thì
“, mệnh đề này sai vì mệnh đề
sai.
Mệnh đề đảo là : ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
sai.
C. Mệnh đề là ” Nếu
thì
“, mệnh đề này sai vì mệnh đề
sai.
Mệnh đề đảo là : ” Nếu
thì
“, mệnh đề này sai vì mệnh đề
sai.
D. Mệnh đề là ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
sai.
Mệnh đề đảo là : ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
sai.
c) ” Tam giác
vuông cân tại A” và
” Tam giác
có
”
A. Mệnh đề là ” Nếu tam giác
vuông cân tại A thì
“, mệnh đề này sai
Mệnh đề đảo là : ” Nếu tam giác
có
thì nó vuông cân tại A”, mệnh đề này sai
B. Mệnh đề là ” Nếu tam giác
vuông cân tại A thì
“, mệnh đề này đúng
Mệnh đề đảo là : ” Nếu tam giác
có
thì nó vuông cân tại A”, mệnh đề này đúng
C. Mệnh đề là ” Nếu tam giác
vuông cân tại A thì
“, mệnh đề này đúng
Mệnh đề đảo là : ” Nếu tam giác
có
thì nó vuông cân tại A”, mệnh đề này sai
D. Mệnh đề là ” Nếu tam giác
vuông cân tại A thì
“, mệnh đề này sai
Mệnh đề đảo là : ” Nếu tam giác
có
thì nó vuông cân tại A”, mệnh đề này đúng
d) ” Ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam” và
” Ngày 27 tháng 7 là ngày thương binh liệt sĩ”
A. Mệnh đề là ” Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam thì ngày 27 tháng 7 là ngày thương binh liệt sĩ” mệnh đề sai
Mệnh đề đảo là : ” Nếu ngày 27 tháng 7 là ngày thương binh liệt sĩ thì ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam” mệnh đề sai
B. Mệnh đề là ” Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam thì ngày 27 tháng 7 là ngày thương binh liệt sĩ” mệnh đề đúng
Mệnh đề đảo là : ” Nếu ngày 27 tháng 7 là ngày thương binh liệt sĩ thì ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam” mệnh đề đúng
C. Mệnh đề là ” Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam thì ngày 27 tháng 7 là ngày thương binh liệt sĩ” mệnh đề này sai
Mệnh đề đảo là : ” Nếu ngày 27 tháng 7 là ngày thương binh liệt sĩ thì ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam”mệnh đề này đúng
D. Mệnh đề là ” Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam thì ngày 27 tháng 7 là ngày thương binh liệt sĩ” mệnh đề này đúng
Mệnh đề đảo là : ” Nếu ngày 27 tháng 7 là ngày thương binh liệt sĩ thì ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam” mệnh đề này sai
Lời giải:
a) Mệnh đề là ” Nếu tứ giác
là hình thoi thì AC và BD cắt nhau tại trung điểm mỗi đường”, mệnh đề này đúng.
Mệnh đề đảo là : “Nếu tứ giác
có AC và BD cắt nhau tại trung điểm mỗi đường thì
là hình thoi “, mệnh đề này sai.
b) Mệnh đề là ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
sai.
Mệnh đề đảo là : ” Nếu
thì
“, mệnh đề này đúng vì mệnh đề
sai.
c) Mệnh đề là ” Nếu tam giác
vuông cân tại A thì
“, mệnh đề này đúng
Mệnh đề đảo là : ” Nếu tam giác
có
thì nó vuông cân tại A”, mệnh đề này sai
d) Mệnh đề là ” Nếu ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam thì ngày 27 tháng 7 là ngày thương binh liệt sĩ”
Mệnh đề đảo là : ” Nếu ngày 27 tháng 7 là ngày thương binh liệt sĩ thì ngày 2 tháng 9 là ngày Quốc Khánh của nước Việt Nam”
Hai mệnh đề trên đều đúng vì mệnh đề đều đúng
DẠNG 3: MỆNH ĐỀ CHỨA BIẾN VÀ MỆNH ĐỀ CHỨA KÍ HIỆU 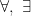 .
.
Các ví dụ minh họa.
Ví dụ 1: Cho mệnh đề chứa biến “” , xét tính đúng sai của các mệnh đề sau:
a)
A. mệnh đề sai B. mệnh đề đúng
C. mệnh đề vừa đúng vừa sai D. Không phải là mệnh đề
b)
A. mệnh đề sai B. mệnh đề đúng
C. mệnh đề vừa đúng vừa sai D. Không phải là mệnh đề
c)
A. mệnh đề sai B. mệnh đề đúng
C. mệnh đề vừa đúng vừa sai D. Không phải là mệnh đề
d)
A. mệnh đề sai B. mệnh đề đúng
C. mệnh đề vừa đúng vừa sai D. Không phải là mệnh đề
Lời giải:
a) Ta có đây là mệnh đề sai
b) Ta có đây là mệnh đề đúng
c) Ta có là mệnh đề sai vì
là mệnh đề sai
d) Ta có là mệnh đề đúng vì
với mọi số tự nhiên.
Ví dụ 2: Dùng các kí hiệu để viết các câu sau và viết mệnh đề phủ định của nó.
a) Với mọi số thực bình phương của là một số không âm.
A. Ta có , mệnh đề phủ định là
B. Ta có , mệnh đề phủ định là
C. Ta có , mệnh đề phủ định là
D. Ta có , mệnh đề phủ định là
b) Có một số nguyên mà bình phương của nó bằng chính nó.
A. , mệnh đề phủ định là
.
B. , mệnh đề phủ định là
.
C. , mệnh đề phủ định là
.
D. , mệnh đề phủ định là
.
c) Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó.
A. , mệnh đề phủ định là
.
B. , mệnh đề phủ định là
.
C. , mệnh đề phủ định là
.
D. , mệnh đề phủ định là
.
Lời giải:
a) Ta có , mệnh đề phủ định là
b) Ta có , mệnh đề phủ định là
.
c) , mệnh đề phủ định là
.











