Hàm số bậc nhất

HÀM SỐ BẬC NHẤT

A. TÓM TẮT LÝ THUYẾT.

1. Định nghĩa: Hàm số bậc nhất là hàm số có dạng $y=ax+b$ $(a\ne 0)$ .

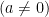2. Sự biến thiên

$\bullet \text{ }$ TXĐ: $D=\mathbb{R}$

$\bullet \text{ }$ Hàm số số đồng biến khi $a>0$ và nghịch biến khi $a<0$

Bảng biến thiên

3. Đồ thị.

Đồ thị của hàm số $y=ax+b$ $(a\ne 0)$ là một đường thẳng có hệ số góc bằng $a$ , cắt trục hoành tại $A\left( -\frac{b}{a};0 \right)$ và trục tung tại $B\left( 0;b \right)$

Chú ý:

$\bullet \text{ }$ Nếu $a=0\Rightarrow y=b$ là hàm số hằng, đồ thị là đường thẳng song song hoặc trùng với trục hoành.

$\bullet \text{ }$ Phương trình $x=a$ cũng là một đường thẳng(nhưng không phải là một hàm số) vuông góc với trục tọa độ và cắt tại điểm có hoành độ bằng a.

$\bullet \text{ }$ Cho đường thẳng $\displaystyle d$ có hệ số góc $k$ , $\displaystyle d$ đi qua điểm $M\left( {{x}_{0}};{{y}_{0}} \right)$ , khi đó phương trình của đường thẳng $d$ là: $y-{{y}_{0}}=a\left( x-{{x}_{0}} \right)$ .

B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.

DẠNG TOÁN 1: XÁC ĐỊNH HÀM SỐ BẬC NHẤT VÀ SỰ TƯƠNG GIAO GIỮA ĐỒ THỊ CÁC HÀM SỐ

1. Phương pháp giải.

$\bullet$ Để xác định hàm số bậc nhất ta là như sau

Gọi hàm số cần tìm là $y=ax+b,\,a\ne 0$ . Căn cứ theo giả thiết bài toán để thiết lập và giải hệ phương trình với ẩn $\displaystyle a,\,b$ , từ đó suy ra hàm số cần tìm.

$\bullet$ Cho hai đường thẳng $\displaystyle {{d}_{1}}:y={{a}_{1}}x+{{b}_{1}}$ và $\displaystyle {{d}_{2}}:y={{a}_{2}}x+{{b}_{2}}.$ Khi đó:

a) $\displaystyle {{d}_{1}}$ và $\displaystyle {{d}_{2}}$ trùng nhau $\displaystyle \Leftrightarrow \left\{ \begin{array}{l}{{a}_{1}}={{a}_{2}}\\{{b}_{1}}={{b}_{2}}\end{array} \right.;$

b) $\displaystyle {{d}_{1}}$ và $\displaystyle {{d}_{2}}$ song song nhau $\displaystyle \Leftrightarrow \left\{ \begin{array}{l}{{a}_{1}}={{a}_{2}}\\{{b}_{1}}\ne {{b}_{2}}\end{array} \right.;$

c) $\displaystyle {{d}_{1}}$ và $\displaystyle {{d}_{2}}$ cắt nhau $\displaystyle \Leftrightarrow {{a}_{1}}\ne {{a}_{2}}.$ Và tọa độ giao điểm là nghiệm của hệ phương trình

d) $\displaystyle {{d}_{1}}$ và $\displaystyle {{d}_{2}}$ vuông góc nhau $\displaystyle \Leftrightarrow {{a}_{1}}.{{a}_{2}}=-1.$

2. Các ví dụ minh họa.

Ví dụ 1. Cho hàm số bậc nhất có đồ thị là đường thẳng $d$ . Tìm hàm số đó biết:

a) $\displaystyle d$ đi qua $A(1;3),\text{ }B(2;-1)$

A. $y=-4x+2$ B. $y=-2x+3$ C. $y=-4x+5$ D. $y=-4x+7$

b) $d$ đi qua $C(3;-2)$ và song song với $\Delta :3x-2y+1=0$

A. $y=\frac{1}{2}x-\frac{3}{2}$ B. $y=\frac{3}{2}x-\frac{13}{2}$ C. $y=\frac{3}{2}x-\frac{3}{2}$ D. $y=\frac{3}{2}x+\frac{3}{2}$

c) $d$ đi qua $M(1;2)$ và cắt hai tia $Ox,Oy$ tại $P,Q$ sao cho ${{S}_{\Delta OPQ}}$ nhỏ nhất.

A. $y=-2x+2$ B. $y=-2x+3$ C. $y=-2x+4$ D. $y=2x-1$

d) $d$ đi qua $N\left( 2;-1 \right)$ và $d\bot d'$ với $d':y=4x+3$ .

A. $y=-\frac{1}{4}x-\frac{1}{2}$ B. $y=-\frac{1}{4}x-\frac{1}{3}$ C. $y=-\frac{1}{4}x+\frac{1}{2}$ D. $y=\frac{1}{4}x-\frac{1}{2}$

Lời giải:

Gọi hàm số cần tìm là $y=ax+b,\,a\ne 0$

a) Vì $A\in d$ và $B\in d$ nên ta có hệ phương trình

Vậy hàm số cần tìm là y = -4x + 7

b) Ta có . Vì $\displaystyle \text{d}//\Delta$ nên (1)

Mặt khác C ∈ d ⇒ -2 = 3a + b (2)

Từ (1) và (2) suy ra

Vậy hàm số cần tìm là $y=\frac{3}{2}x-\frac{13}{2}$

c) Đường thẳng $\displaystyle d$ cắt trục $\displaystyle Ox$ tại $P\left( -\frac{b}{a};0 \right)$ và cắt $\displaystyle \text{O}y$ tại $Q\left( 0;b \right)$ với $a<0,\,\,b>0$

Suy ra ${{S}_{\Delta OPQ}}=\frac{1}{2}OP.OQ=\frac{1}{2}.\left| -\frac{b}{a} \right|.\left| b \right|=-\frac{{{b}^{2}}}{2a}$ (3)

Ta có $M\in d\Rightarrow 2=a+b\Rightarrow b=2-a$ thay vào (3) ta được

$\displaystyle {{S}_{\Delta OPQ}}=-\frac{{{\left( 2-a \right)}^{2}}}{2a}=-\frac{2}{a}-\frac{a}{2}+2$

Áp dụng bất đẳng thức côsi ta có

$\displaystyle -\frac{2}{a}-\frac{a}{2}\ge 2\sqrt{\left( -\frac{2}{a} \right).\left( -\frac{a}{2} \right)}=2\Rightarrow {{S}_{\Delta OPQ}}\ge 4$

Đẳng thức xảy ra khi và chỉ khi

Vậy hàm số cần tìm là $y=-2x+4$ .

d) Đường thẳng $d$ đi qua $N\left( 2;-1 \right)$ nên $-1=2a+b$ (4)

Và $d\bot d'\Rightarrow 4.a=-1\Leftrightarrow a=-\frac{1}{4}$ thay vào (4) ta được $b=-\frac{1}{2}$ .

Vậy hàm số cần tìm là $y=-\frac{1}{4}x-\frac{1}{2}$ .

Ví dụ 2: Cho hai đường thẳng $\,d:y=x+2m,\,\,d':y=3x+2$ ( $m$ là tham số)

a) Chứng minh rằng hai đường thẳng $d,\,\,d'$ cắt nhau và tìm tọa độ giao điểm của chúng

A. $M\left( 2m-1;3m-1 \right)$ B. $M\left( m-2;3m-2 \right)$

C. $M\left( m+1;3m+1 \right)$ D. $M\left( m-1;3m-1 \right)$

b) Tìm $m$ để ba đường thẳng $d,\,d'$ và $d'':y=-mx+2$ phân biệt đồng quy.

A. $m=-1$ B. $m=3$ C. $m=1$ D. $m=2$

Lời giải:

a) Ta có ${{a}_{d}}=1\ne {{a}_{d'}}=3$ suy ra hai đường thẳng $d,\,\,d'$ cắt nhau.

Tọa độ giao điểm của hai đường thẳng $d,\,\,d'$ là nghiệm của hệ phương trình

suy ra $d,\,\,d'$ cắt nhau tại $M\left( m-1;3m-1 \right)$

b) Vì ba đường thẳng $d,\,\,d',\,\,d''$ đồng quy nên $M\in d''$ ta có

$3m-1=-m\left( m-1 \right)+2\Leftrightarrow {{m}^{2}}+2m-3=0$ ⇔ m = 1, m = -3.

$\bullet$ Với $m=1$ ta có ba đường thẳng là $\,\,d:y=x+2,\,\,d':y=3x+2,\,\,d'':y=-x+2,$ phân biệt và đồng quy tại $M\left( 0;2 \right)$ .

$\bullet$ Với $m=-3$ ta có $\displaystyle d'\equiv d''$ suy ra $m=-3$ không thỏa mãn

Vậy $m=1$ là giá trị cần tìm.

Ví dụ 3: Cho đường thẳng $d:\,\,y=\left( m-1 \right)x+m$ và $d':y=\left( {{m}^{2}}-1 \right)x+6$

a) Tìm $m$ để hai đường thẳng $\displaystyle d,\,\,d'$ song song với nhau

A. $m=0$ và $m=3$ B. $m=0$ và $m=2$ C. $m=0$ và $m=1$ D. $m=0$ và $m=4$

b) Tìm $m$ để đường thẳng $\displaystyle d$ cắt trục tung tại $A$ , $\displaystyle d'$ cắt trục hoành tại $B$ sao cho tam giác $OAB$ cân tại $O$

A. $m=\pm 4$ B. $m=\pm 2$ C. $m=\pm 3$ D. $m=\pm 1$

Lời giải:

a) Với $m=1$ ta có $\displaystyle d:\,\,y=1,\,\,d':y=6$ do đó hai đường thẳng này song song với nhau

Với $m=-1$ ta có $\displaystyle d:\,\,y=-2x-1,\,\,d':y=6$ suy ra hai đường thẳng này cắt nhau tại $M\left( -\frac{7}{2};6 \right)$

Với $m\ne \pm 1$ khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi

Đối chiếu với điều kiện $m\ne \pm 1$ suy ra $m=0$ .

Vậy $m=0$ và $m=1$ là giá trị cần tìm.

b) Ta có tọa độ điểm $A$ là nghiệm của hệ

DẠNG TOÁN 2: XÉT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ CỦA HÀM SÔ BẬC NHẤT.

1. Các ví dụ minh họa.

Ví dụ 1: Lập bảng biến thiên và vẽ đồ thị của các hàm số sau

a) $y=3x+6$

b) $y=-\frac{1}{2}x+\frac{3}{2}$

Lời giải:

a) TXĐ: $\displaystyle \text{D}=\mathbb{R}$ , $a=3>0$ suy ra hàm số đồng biến trên $\mathbb{R}$

Bảng biến thiên

Đồ thị hàm số $y=3x+6$ đi qua $A\left( -2;0 \right),\,\,B\left( -1;3 \right)$

b) TXĐ: $\displaystyle \text{D}=\mathbb{R}$ , $a=-\frac{1}{2}<0$ suy ra hàm số nghịch biến trên $\mathbb{R}$

Bảng biến thiên

Đồ thị hàm số $y=-\frac{1}{2}x+\frac{3}{2}$ đi qua $A\left( 3;0 \right),\,\,B\left( 0;\frac{3}{2} \right)$

Ví dụ 2. Cho các hàm số : $y=2x-3,\,\,y=-x-3,\,\,y=-2$ .

a) Vẽ đồ thị các hàm số trên

b) Dựa vào đồ thị hãy xác định giao điểm của các đồ thị hàm số đó.

Lời giải:

a) Đường thẳng y = 2x - 3 đi qua các điểm

Đường thẳng $y=-x-3$ đi qua các điểm A(0; -3), C(-3; 0)

Đường thẳng $y=-2$ song song với trục hoành và cắt trục tung tại điểm có tung độ bằng -2

b) Đường thẳng $y=2x-3,\,\,y=-x-3$ cắt nhau tại $A\left( 0;-3 \right)$ , Đường thẳng $y=-x-3,\,\,y=-2$ cắt nhau tại $A'\left( -1;-2 \right)$ , Đường thẳng $y=2x-3,\,\,y=-2$ cắt nhau tại $A''\left( \frac{1}{2};-2 \right)$ .

Ví dụ 3: Cho đồ thị hàm số có đồ thị (hình vẽ)

a) Hãy lập bảng biến thiên của hàm số trên $\left[ -3;3 \right]$

b) Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên

Lời giải:

a) Bảng biến thiên của hàm số trên $\left[ -3;3 \right]$

b) Dựa vào đồ thị hàm số đã cho ta có:

khi và chỉ khi $x=-4$

$\displaystyle \underset{\left[ -4;2 \right]}{\mathop{\min }}\,=0$ khi và chỉ khi

DẠNG TOÁN 3: ĐỒ THỊ CỦA HÀM SỐ CHỨA DẤU TRỊ TUYỆT ĐỐI $y=\left| ax+b \right|$ .

1. Phương pháp giải.

Vẽ đồ thị của hàm số $y=\left| ax+b \right|$ ta làm như sau

Cách 1: Vẽ là đường thẳng $y=ax+b$ với phần đồ thị sao cho hoành độ thỏa mãn $\displaystyle x\ge -\frac{b}{a}$ , Vẽ $\left( {{C}_{2}} \right)$ là đường thẳng $y=-ax-b$ lấy phần đồ thị sao cho . Khi đó là hợp của hai đồ thị $\left( {{C}_{1}} \right)$ và $\left( {{C}_{2}} \right)$ .

Cách 2: Vẽ đường thẳng $y=ax+b$ và $y=-ax-b$ rồi xóa đi phần đường thẳng nằm dưới trục hoành. Phần đường thẳng nằm trên trục hoành chính là $\left( C \right)$ .

Chú ý:

$\bullet$ Biết trước đồ thị $\displaystyle \left( C \right):y=f\left( x \right)$ khi đó đồ thị $\displaystyle \left( {{C}_{1}} \right):y=f\left( \left| x \right| \right)$ là gồm phần :

– Giữ nguyên đồ thị $\displaystyle \left( C \right)$ ở bên phải trục tung;

– Lấy đối xứng đồ thị $\displaystyle \left( C \right)$ ở bên phải trục tung qua trục tung.

Biết trước đồ thị $\displaystyle \left( C \right):y=f\left( x \right)$ khi đó đồ thị là gồm phần:

– Giữ nguyên đồ thị $\displaystyle \left( C \right)$ ở phía trên trục hoành

– Lấy đối xứng đồ thị ở trên dưới trục hoành và lấy đối xứng qua trục hoành.

2. Các ví dụ minh họa.

Ví dụ 1. Vẽ đồ thị của các hàm số sau

a) $\displaystyle y=\left\{ \begin{array}{l}2x\quad khi\ x\ge 0\\-x\quad khi\ x<0\end{array} \right.$ . b).

Lời giải:

a) Với $x\ge 0$ đồ thị hàm số y = 2x là phần đường thẳng đi qua hai điểm $O\left( 0;0 \right),\,\,A\left( 1;2 \right)$ nằm bên phải của đường thẳng x = 0.

Với $\displaystyle x<0$ đồ thị hàm số y = -x là phần đường thẳng đi qua hai điểm $B\left( -1;1 \right),\,\,C\left( -2;2 \right)$ nằm bên trái của đường thẳng x = 0.